Un'equazione si dice di secondo grado quando la x vi compare a potenza 2, cioè c'è un termine con x².
Spiegazione
Data un'equazione di secondo grado nella seguente forma:

a, b, c = sono la parte numerica dell'equazione
Dove...
a = coefficiente x²
b = coefficiente x
c = termine noto.
x = è l'incognita
L'equazione può ammettere 2 soluzioni distinte, una sola soluzione oppure non ammette soluzioni.
Le formule risolutive generali delle equazioni di secondo grado sono:
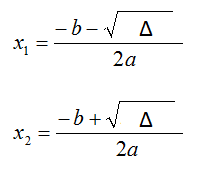
Ricordo che il discriminante (delta) è ciò che si trova sotto la radice e si indica con il simbolo Δ, ovvero un triangolo. Il delta si calcola usando la seguente Formula:

Quindi va sostituito il delta con la relativa formuletta:

Le equazioni possono anche essere scomposte con le semplici regole matematiche che dovreste già conoscere e, quindi una volta scomposte in fattori è semplice trovare le soluzioni.
Si chiama discriminante poiché le possibili soluzioni dell'equazione quadratica dipendono da esso. Si possono verificare infatti tre casi:
Δ > 0 l'equazione ha due soluzioni reali e distinte. La parabola interseca 2 punti sull'asse delle ascisse (x1 e x2).
Δ = 0 l'equazione ha una sola soluzione reale. Se ha solo una soluzione il vertice della parabola coincide con un solo punto dell'asse delle x.
Δ < 0 l'equazione non ha soluzioni reali. Se non ammette soluzioni la parabola non tocca l'asse delle ascisse.

Spiegazione
Data un'equazione di secondo grado nella seguente forma:

a, b, c = sono la parte numerica dell'equazione
Dove...
a = coefficiente x²
b = coefficiente x
c = termine noto.
x = è l'incognita
L'equazione può ammettere 2 soluzioni distinte, una sola soluzione oppure non ammette soluzioni.
Le formule risolutive generali delle equazioni di secondo grado sono:
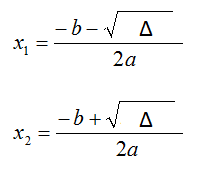
Ricordo che il discriminante (delta) è ciò che si trova sotto la radice e si indica con il simbolo Δ, ovvero un triangolo. Il delta si calcola usando la seguente Formula:

Quindi va sostituito il delta con la relativa formuletta:

Le equazioni possono anche essere scomposte con le semplici regole matematiche che dovreste già conoscere e, quindi una volta scomposte in fattori è semplice trovare le soluzioni.
Si chiama discriminante poiché le possibili soluzioni dell'equazione quadratica dipendono da esso. Si possono verificare infatti tre casi:
Δ > 0 l'equazione ha due soluzioni reali e distinte. La parabola interseca 2 punti sull'asse delle ascisse (x1 e x2).
Δ = 0 l'equazione ha una sola soluzione reale. Se ha solo una soluzione il vertice della parabola coincide con un solo punto dell'asse delle x.
Δ < 0 l'equazione non ha soluzioni reali. Se non ammette soluzioni la parabola non tocca l'asse delle ascisse.

Tipi di equazioni
A seconda dei termini presenti, oltre a quello di secondo grado, le equazioni possono essere suddivise in pure, spurie e complete.
- Nelle equazioni pure b= 0, quindi basta fare 4ac
- In quelle spurie c= 0, quindi basta fare b²
- L'equazione usata nell'esempio si dice completa perché è presente la parte numerica e quindi ha un valore diverso da zero: ax² + bx + c= 0
GUARDA ANCHE: Risolvere equazioni di secondo grado online












