
Le equazioni di secondo grado sono diventate il tuo nuovo incubo? Niente paura, sul nostro sito potete fare affidamento sul nostro strumento per verificare il corretto risultato delle equazioni di secondo grado online. Quando presenti calcola le due soluzioni sia sotto forma di frazione sia sotto forma di numero decimale e, inoltre, esegue anche il calcolo del delta. In fondo alla pagina è presente una spiegazione per capire come si usa lo strumento e anche un breve ripasso di teoria riguardante le equazioni di secondo grado.
Risolvere equazione di secondo grado online
Come si usa il calcolatore?
Il funzionamento di questo strumento che risolve le equazioni di secondo grado online e in modo totalmente gratuito è semplicissimo! Tutto quello che dovete fare è inserire il valore corrispondente a ogni coefficiente e poi cliccare sul pulsante "Calcola". Nel risultato trovere il valore del delta e a seconda dei casi, cioè se è maggiore, uguale o minore di 0 vi apparirà il calcolo delle soluzioni dell'equazione. Quando le soluzioni sono numeri decimali, vi apparirà anche la versione della soluzione sotto forma di frazione dato che per alcuni esercizi è meglio lavorare con le frazioni che con i numeri decimali.Equazioni di secondo grado: ripasso rapido
Un'equazione di secondo grado è anche chiamata equazione quadratica perché un'incognita ha un esponente elevato a 2, cioè al quadrato. La forma normale delle equazioni di secondo grado è la seguente:La formula risolutiva delle equazioni di secondo grado è la seguente:
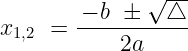
Il simbolo del delta (lettera greca), chiamato anche discriminante, è il valore posto sotto la radice quadrata.
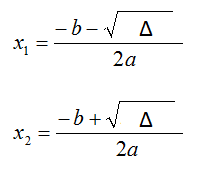
Il delta corrisponde a uno specifico calcolo che coinvolge tutti e quattro i coefficienti:
Quando il valore del delta è positivo o maggiore di zero (Δ > 0), vi sono due soluzioni reali e distinte (x1 e x2). Le soluzioni sono due perché appena prima della radice quadrata è presente il simbolo (±), cioè dovete applicare una prima volta la formula utilizzando il segno dell'addizione e una seconda volta utilizzando il segno della sottrazione. Quando il delta è uguale a zero (Δ = 0), dal momento che la radice quadrata è zero, vi sono due soluzioni ma coincidenti (cioè con lo stesso valore), dunque basta effettuare il calcolo o con l'addizione o con la sottrazione, è indifferente. Quando il delta è negativo o minore di zero (Δ < 0) l'equazione è impossibile perché non ammette soluzioni reali.












